HEIDENHAIN iTNC 530 (340 49x-03) ISO programming - Instrukcja (Strona 106)

106 4 Programowanie: podstawy, zarządzanie plikami, pomoce przy programowaniu, zarządzanie paletami
4.1 Podstawy
Wyspółrzędnych biegunowych
Jeżeli rysunek wykonawczy jest wymiarowany prostokątnie, proszę
napisać program obróbki także ze współrzędnymi prostokątnymi. W
przypadku przedmiotów z łukami kołowymi lub przy podawaniu
wielkości kątów, łatwiejsze jest ustalenie położenia przy pomocy
współrzędnych biegunowych.
W przeciwieństwie do współrzędnych prostokątnych X,Y i Z,
współrzędne biegunowe opisują tylko położenie na jednej
płaszczyźnie. Współrzędne biegunowe mają swój punkt zerowy na
biegunie CC (CC = circle centre; angl. środek koła). Pozycja w jednej
płaszczyźnie jest jednoznacznie określona przez:
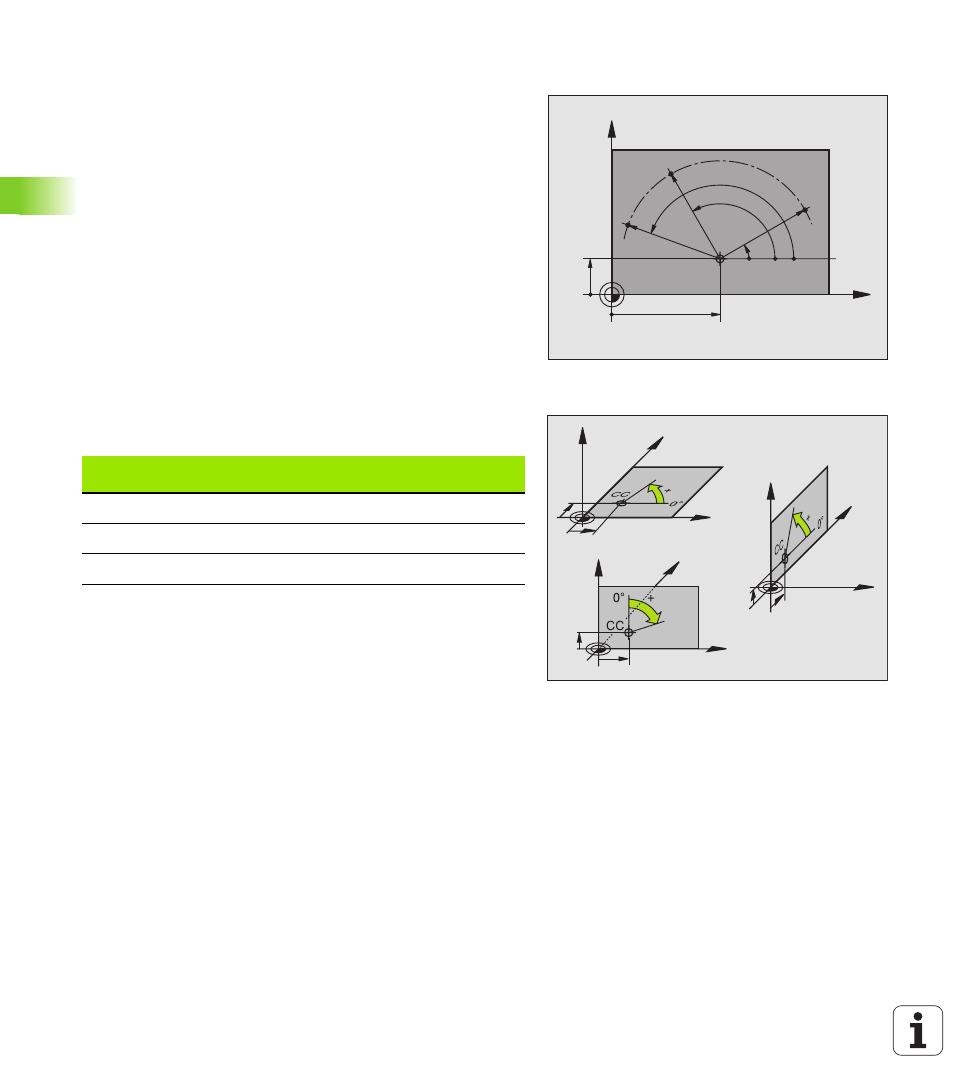
„ Współrzędne biegunowe-promień: odstęp od bieguna CC do pozycji
„ Współrzędne biegunowe-kąt: kąt pomiędzy osią odniesienia kąta i
odcinkiem łączącym biegun CC z daną pozycją.
Patrz ilustracja po prawej stronie u góry
Określenie bieguna i osi odniesienia kąta
Biegun określa się przy pomocy dwóch współrzędnych w
prostokątnym układzie współrzędnych na jednej z trzech płaszczyzn.
Tym samym jest także jednoznacznie zaszeregowana oś odniesienia
kąta dla kąta współrzędnych biegunowych PA.
X
Y
0°
30
10
CC
R
H
1
H
2
R
R
H
3
X
Z
Y
X
Z
Y
X
Z
Y
I
J
K
K
J
I
Współrzędne bieguna
(płaszczyzna)
Oś odniesienia kąta
X/Y +X
Y/Z +Y
Z/X +Z